Algoritmos Probabilísticos 2022 - 1
Jair Donadelli — email jair.donadelli ‘arroba’ ufabc. …

Algoritmos aleatorizados nasceram como uma ferramenta na teoria computacional dos números e evoluiram rapidamente para um conjunto de ferramentas e técnicas com ampla aplicação desde criptografia até a teoria da aprendizagem computacional. Esta disciplina apresenta os conceitos básicos de algoritmos aleatorizados em um nível acessível a alunos avançados no curso de graduação. A disciplina está organizada em três linhas principais: as ferramentas e técnicas probabilísticas, os fundamentos computacionais e áreas específicas de aplicação. Pré-requisitos: Introdução a Probabilidade e Estatística; Análise de Algoritmos.
Se está matriculado, atente para seu email institucional. Esta disciplina está no moodle
Algoritmos Probabilísticos 2022 - 1EmentaObjetivosReferênciasAvaliaçãoAtendimentoProgramação (em construção)Calendário acadêmico
Ementa
Ferramentas e Técnicas: Teoria básica da probabilidade; Markov, Chebyshev e desigualdades de momento; problemas de coleção de cupons e ocupação ; desigualdades de cauda e limites de Chernoff; expectativa condicional e martingais; cadeias de Markov e passeios aleatórios. Fundamentos: teoria da complexidade probabilística; técnicas de teoria dos jogos; problemas de aproximação e contagem; amplificação de probabilidade e desaleatorização. Aplicações: classificação e busca; estruturas de dados; otimização combinatória e algoritmos de grafos; algoritmos para conjuntos de dados massivos, incluindo busca por similaridade, vizinhos mais próximos e agrupamento; algoritmos em teoria dos números.
Objetivos
Possibilitar o aluno compreender os modelos probabilísticos de computação, seu poder e suas limitações, capacitar no uso desses modelos em problemas computacionais e no uso das ferramentas mais comuns da probabilidade para a análise de desempenho e limitação da probabilidade de erro.
Referências
 Básicas
Básicas
- Probablility and Computing, M. MITZENMACHER, E. UPFAL.
- Randomized Algorithms, R. MOTWANI e P. RAGHAVAN.
Complementares
- Computational Complexity: A Modern Approach, S. ARORA, B BARAK.
- Design and Analysis of Randomized Algorithms, J. HROMKOVIC.
- Concentration of measure for the analysis of randomized algorithms DUBHASHI e DEVSATT.
Auto-ajuda
R. Bianconi, Como ler e estudar matemática?
Fernando Q. Gouvêa e Shai Simonson, How to Read Mathematics (uma tradução “rápida e grosseira”, segundo o tradutor, aqui).
Avaliação
 Provas
Provas
Atendimento
 4ªs as 18h00, ou em horário agendado por email.
4ªs as 18h00, ou em horário agendado por email.
Programação (em construção)
Oficialmente, as aulas são nas 3as as 10h00 e 5as 08h00. Na ultima oferta a programação está aqui.
| Semana | Tema | Atividade | |
|---|---|---|---|
| 01 | Apresentação da disciplina. Dois exemplos: testes de identidade de produto de matrizes e polinômios. Desaleatorização. Revisão de análise de algoritmos. | Video aula Leitura de texto Discussão no Fórum | |
| 02 | Revisão de espaços de probabilidade, probabilidade condicional e independência. Gerador de números aleatórios a partir de bits aleatórios. | Video aula Leitura de texto Discussão no Fórum | |
| 03 | Variáveis aleatórias, esperança, distribuições geométrica e binomial, análise do quicksort probabilístico. | Video aula Leitura de texto Discussão no Fórum | |
| 04 | Método probabilístico 1º momento; max-e3sat; , esperança condicional e desaleatorização. | Video aula Leitura de texto Discussão no Fórum | |
| 05 | Método probabilístico 2º momento; problemas de ocupação; transição de fase. | Video aula Leitura de texto Discussão no Fórum | |
| 06 | Modelos de computação, maquina turing probabilistica; classes de complexidade, P, NP, BPP, P/poly. | Video aula Leitura de texto Discussão no Fórum | |
| 07 | Criptografia; funções one-way; geradores pseudoaleatórios seguros;criptografia de chave pública. Provas com conhecimento zero. | Video aula Leitura de texto Discussão no Fórum | |
| 08 | Avaliação | ||
| 09 | Passeios aleatórios em grafos. | ||
| 10 | Passeios aleatórios em grafos. | ||
| 11 | leis de desvios | ||
| 12 | leis de desvios |
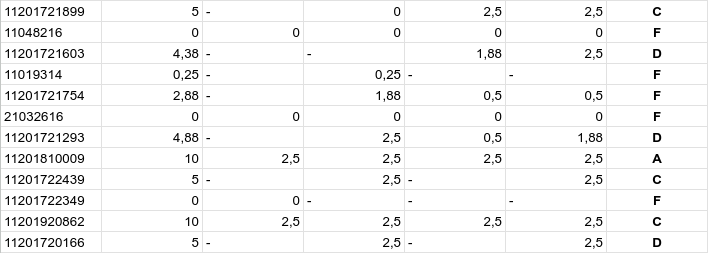
Resultado