1 Equações e Inequações
1.1 Polinômios
O Maxima é capaz de manipular polinômios e outras expressões
simbólicas. Para mostrar ao Maxima um polinômio, basta digitá-lo:
| (%i1) | x^2-x; |
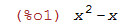
No entanto, ao digitar um polinômio, devemos usar o sinal * para
multiplicação (o Maxima não entende que ``2a'' é o mesmo que
``2 vezes a'':
| (%i2) | 10 * x^3-8 * x^2+5; |
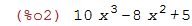
Vimos no Capítulo anterior como definir variáveis. O Maxima pode
guardar em uma variável não apenas números, mas qualquer objeto
matemático -- inclusive polinômios!
| (%i3) | p: x^2*(2*x-3) +3*(x-4+x) +8; |
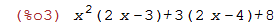
O nome p agora se refere a este polinômio:;
| (%i4) | p; |
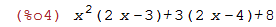
1.2 Simplificando e expandindo polinômios
O Maxima pode simplificar ou expandir polinômios usando a função expand
Ao expandir, o Maxima:
* Desenvolverá produtos e potências de somas: por exemplo, $a(b+c)$ será
reescrito como $ab+ac$ e $(a+b)^2$ será expandido para $a^2+2ab+b^2$;
* Separará números racionais onde há soma no numerador,
reescrevendo como dois números. Por exemplo, $(a+b)/c$ é
transformado em $a/c + b/c$;
* Aplicará a propriedade distributiva em multiplicações, dando
origem a mais termos. Por exemplo, $a(b+c)$ se torna $ab+ac$.
| (%i5) | ex: (a+b)*(a+c); |
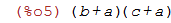
| (%i6) | expand(ex); |
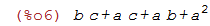
A função ratsimp tenta simplificar polinômios.
Podemos usar ratsimp para simplificar o polinômio p
(que já definimos) usando seu nome:
| (%i7) | ratsimp(p); |
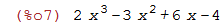
A função ratsimp não alterou a forma do polinômio p. Ela apenas
encontrou uma versão simplificada do polinômio e a mostrou na tela. O
polinômio p continua guardado na mesma forma que antes:
| (%i8) | p; |
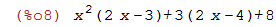
A função factorsum é especialmente útil quando temos uma
expressão muito grande e queremos verificar rapidamente se ela pode
ser fatorada:
| (%i9) |
expressao: b*d^2*e+a*d^2*e+2*b*c*d*e+2*a*c*d*e+b*c^2*e+ a*c^2*e+5*b*d^2+5*a*d^2+10*b*c*d+10*a*c*d+5*b*c^2+5*a*c^2; |
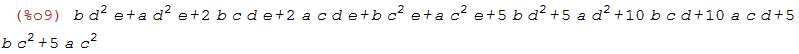
| (%i10) | factorsum(expressao); |
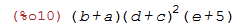
1.3 Resolvendo Equações
O Maxima simplesmente nos devolveu a equação, sem resolvê-la. A equação é
um ``objeto matemático'' para o Maxima, e ele somente o manipulará se
pedirmos explicitamente. A função solve encontra soluções para
equações e as devolve em uma lista:
| (%i11) | solve(x^2+10*x+8=0,x); |
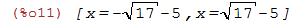
Podemos também encontrar os pontos em que duas funções coincidem.
No exemplo a seguir daremos ao Maxima dois polinômios, descrevendo
uma reta e uma parábola.
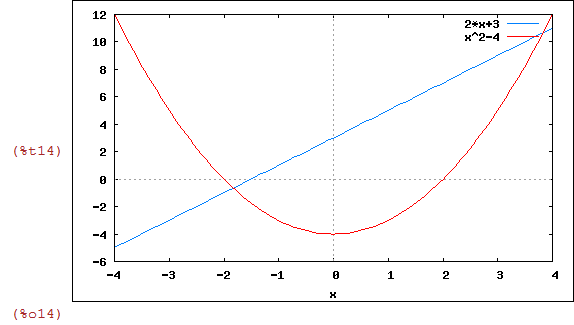
| (%i12) | reta: 2*x+3; |

| (%i13) | para: x^2-4; |
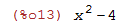
Tendo dado nomes aos dois polinômios, podemos então plotá-los e
visualizar os pontos onde a reta e a parábola se interceptam:
| (%i14) | wxplot2d([reta,para],[x,-4,4]); |
Se pedirmos para resolver para=reta, o Maxima mostrará os pontos
onde ambas se interceptam:
| (%i15) | solve(para=reta); |
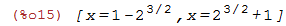
Também podemos verificar os zeros de ambos:
| (%i16) | solve(reta=0); |
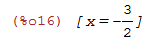
| (%i17) | solve(para=0); |
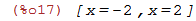
1.4 Sistemas Lineares: Lineares e Modulares
Além de equações, a função solve também resolve sistemas de equações lineares. Basta que
passemos como primeiro argumento o sistema de equações como uma lista:
| (%i18) | solve([x+y=2, 2*x-y=4]); |
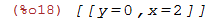
O sistema 2x2 que acabamos de resolver é composto de duas
equações afim. Podemos plotá-las e visualizar o ponto onde se interceptam.
Para isto devemos reescrever ambas na forma y = f(x) -- e o próprio Maxima o
fará se pedirmos que resolva cada linha do sistema para y:
| (%i19) | solve(x+y=2,y); |
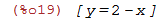
| (%i20) | solve(2*x-y=4,y); |
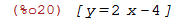
Finalmente, plotamos as duas funções:
| (%i21) | wxplot2d([2-x, 2*x-4],[x,-2,4]); |
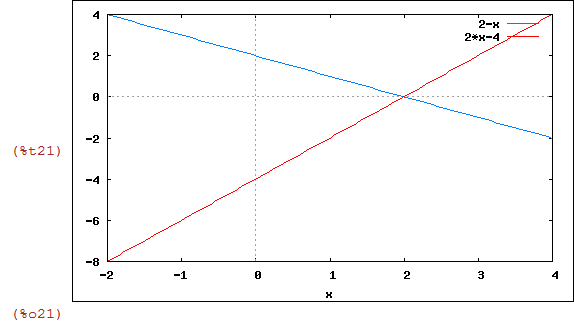
1.5 Resolvendo Inequações
Para que o Maxima resolva inequações, é necessário carregar o módulo fourier_elim (o
módulo tem este nome porque usa o processo de eliminação de Fourier-Motzkin
para resolver sistemas de inequações lineares:
| (%i22) | load(fourier_elim); |
O Maxima então pode calcular as soluções para inequações.
Primeiro uma inequação simples 3x-10-x>0
| (%i23) | fourier_elim([3*x-10-x>0],[x]); |
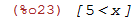
Uma inequação com módulo |3x-10|-x>0:
| (%i24) | fourier_elim([abs(3*x-10)-x>0],[x]); |
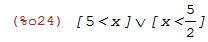
Uma inequação com dois módulos, um dentro do outro:
| (%i25) | fourier_elim(abs(x - abs(4-x)) < 2,[x]); |
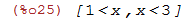
O segundo argumento para fourier_elim foi [x], uma lista contendo x$
Esta lista contém as variáveis que o Maxima levará em consideração ao resolver as
inequações. Para ilustrar isto, usaremos uma inequação com duas variáveis, xy>5x$
| (%i26) | fourier_elim(x * y > 5*x,[x]); |
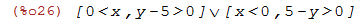
A resposta do Maxima mostra diversas inequações, mas em todas as que envolvem x ele
aparece isolado.
Se passarmos [y] para fourier\_elim,
o Maxima resolverá a inequação para y:
| (%i27) | fourier_elim(x * y > 5*x,[y]); |
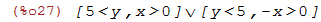
Desta vez temos y isolado em duas das inequações. Podemos pedir também que o Maxima
resolva a inequação para x e y:
| (%i28) | fourier_elim(x * y > 5*x,[x,y]); |
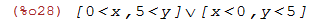
Também é possível resolver um sistema de inequações.
| (%i29) | fourier_elim([abs(x - abs(4-x)) < 2, x > 2],[x]); |
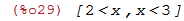
Usando sistemas de inequações fica mais claro porque passamos a lista de
variáveis no segundo argumento de \comando{fourier\_elim}:
| (%i30) | fourier_elim([x + y > 0, x - y < 5],[x]); |
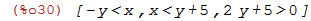
| (%i31) | fourier_elim([x + y > 0, x - y < 5],[y]); |
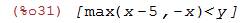
| (%i32) | fourier_elim([x + y > 0, x - y < 5],[x,y]); |
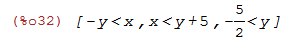
Created with wxMaxima.