Máxima
1 Breve histórico
O Maxima é derivado do sistema Macsyma, desenvolvido no MIT nos anos de 1968 a 1982
como parte do Projecto MAC.
O MIT transferiu uma cópia do código fonte do Macsyma para o Departamento de Energia em 1982;
essa versão é agora conhecida como Macsyma DOE.
Uma cópia do Macsyma DOE foi mantida pelo Professor William F. Schelter da Universidade do Texas, d
esde 1982 até a sua morte em 2001. Em 1998, Schelter obteve autorização do
Departamento de Energia para liberar o código fonte do Macsyma DOE sob a Licença Pública GNU,
e em 2000 iniciou o projeto Maxima no SourceForge para manter e desenvolver o Macsyma DOE, agora chamado Maxima.
2 Introdução ao Máxima
2.1 Operações Aritméticas
Com o Máxima é possível fazer operações aritméticas de modo análogo à uma calculadora:
| (%i1) | 7.53+5.22; |
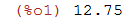
Observe que os comandos do Maxima terminam com ;
e os comentários começam com /* e terminam com */
Vários comandos podem ser inseridos na mesma linha, desde que separados por ponto e virgula:
| (%i2) | 12.4+5; 16+45; |
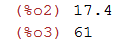
PRODUTO E DIVISÂO
No máxima e * e / representam o produto e a divisão:
| (%i4) | 72*65; |
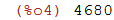
| (%i5) | 76/33.7; |
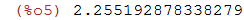
POTÊNCIA
No máxima ^ representa a potência, assim por exemplo 2^10 pode ser calculado:
| (%i6) | 2^10; |
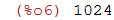
Por exemplo, para calcularmos: (33.1+22.4)^(1/2)
| (%i7) | (33.1+22.4)^(1/2); |
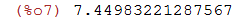
Por exemplo, para entrarmos a expressão: (1+(b+1)^3)(1+b)^2
| (%i8) | (1+(b+1)^3)*(1+b)^2; |
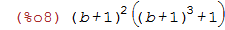
2.2 Valores Exatos e Aproximados
O exemplo abaixo mostra que para divisão de inteiros o Máxima apenas simplifica a fração
| (%i9) | 92/22; |

Se no exemplo anterior, desejarmos uma aproximação numérica para $\frac{46}{11}$ podemos obtê-la
usamos o comando para ponto flutuante float() como abaixo:
| (%i10) | float(92/22); |
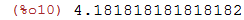
O Maxima interpreta a entrada 22.1 como um número real e realiza as contas envolvendo números reais em ponto flutuante:
| (%i11) | 96/22.1; |
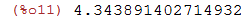
Outro modo de obter a representação decimal de um número real é adicionando uma virgula e o comando numer depois do número real:
| (%i12) | 17/22,numer; |
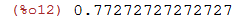
Se desejarmos que os resultados e os cálculos efetuados sejam expressos com um determinado número de casas decimais e/ou
algarismos significativos podemos estabelecer essa precisão mediante a fixação de um
valor à variável interna global fpprec (float point precision, precisão de ponto flutuante),
que por padrão no Máxima é 16)
Para calcularmos as primeiras 30 casas decimais de $pi$, primeiro definimos a precisão de ponto flutuante para 30:
| (%i13) | fpprec:30; |
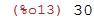
E agora usamos o comando \%pi para acessar a constante pi e bfloat para converter pi em um números flutuante
de grande precisão (bigfloat).
| (%i14) | bfloat(%pi); |
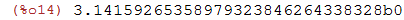
2.3 Constantes Matemáticas
O número \pi deve ser escrito desta forma %pi.
| (%i15) | %pi; |
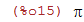
De modo análogo temos que o número de Euler e deve ser escrito como %e
e a constante imaginária i = sqrt(-1) deve ser escrita como %i
| (%i16) | %e,numer; |
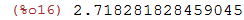
Como exemplo calcularemos e^(pi*i):
| (%i17) | %e^(%pi*%i); |
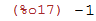
Números Complexos podem ser escritos utilizando a constante \%i
Assim por exemplo podemos calcular o produto entre 2+3i e 4+2i
| (%i18) | (3+3*%i)*(4+5*%i); |
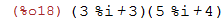
Para que o Maxima expanda o produto anterior podemos usar o comando expand:
| (%i19) | expand((3+3*%i)*(4+5*%i)); |
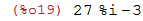
2.4 Algumas Funções Matemáticas
* sqrt(x) denota a raiz quadrada de x
* abs(x) denota módulo de de x
* n! denota fatorial de n
* exp(x) denota a função exponencial de x, i.e, e^x
* log(x) denota o logaritmo natural de x
* sin(x) denota a função seno de x (em radianos)
* cos(x) denota a função cosseno de x
(em radianos)
* tan(x) denota a função tangente de x
* asin(x) denota a função arco-seno de x
* acos
denota a função arco-cosseno de x
Para calcularmos 12!
| (%i20) | 12!; |
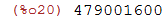
Para calcularmos cos(pi/4);
| (%i21) | cos(%pi/4); |

O Maxima não possui uma função pré-definida para logaritmo de base 10 ou de outras bases.
Podemos definir o logaritmo na base 10 através do comando
| (%i22) | log10(x) := log(x) / log(10); |
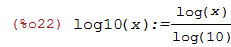
Agora podemos calcular log_10(100)
| (%i23) | log10(100),numer; |
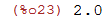
2.5 Usando os Resultados Anteriores
Para convertemos a saída anterior para um valor numérico podemos utilizar o comando
float(\%). Nesse caso o símbolo % nos permite acessar a última saída apresentada:
| (%i24) | cos(%pi/4); |

| (%i25) | float(%); |
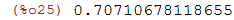
2.6 Definindo Variáveis
Uma ferramenta importante no Maxima é a capacidade de atribuir e manipular
variáveis. Uma variável, em programação, é um identificador ao qual se pode atribuir valores.
No Maxima a instrução de atribuição concretiza-se empregando o símbolo :
| (%i26) | x:3; |
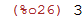
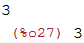
Para visualizar o valor da variável x, utilizamos o comando print.
| (%i27) | print(x); |
Vamos definir y=5 e calcular x+y e x^y+y^x
| (%i28) | y:5; |
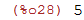
| (%i29) | x+y; |
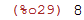
| (%i30) | x^y+y^x; |
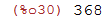
Se desejarmos remover um valor atribuído a uma variável podemos fazer isso através do comando kill:
Esse comando sempre retorna done (i.e. feito);
Para limpar a variável x definida acima:
| (%i31) | kill(x); |
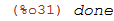
Agora, se retornarmos o valor da variável x, utilizamos o comando print, teremos
| (%i32) | print(x); |

Uma variável pode armazenar expressões.
Assim por exemplo podemos armazenar a expressão pi*a^2*h na variável V através do comando
| (%i33) | V:%pi*a^2*h; |
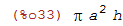
Usando o caractere $ podemos evitar que o máxima exiba uma sáida:
| (%i34) | z:y+7$ |
Se quisermos visualizar o valor da variavél z, :
| (%i35) | print(z); |

Uma variável pode também armazenar uma igualdade ou uma desigualdade.
Se queremos armazenar a desigualdade 3a+5b<3 para usos futuros:
| (%i36) | desigualdade:3*a+5*b<3; |
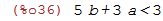
2.7 Somátorios e Produtórios
Para calcular a soma de 1 até 30 de n^2
| (%i37) | sum(n^2,n,1,30); |
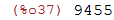
Para calcular a soma de 1 até 10 de 1/(2^n)
| (%i38) | sum(1/2^n,n, 1, 10); |
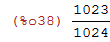
| (%i39) | float(%); |
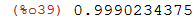
O máxima também aceita somas infinitas:
| (%i40) | sum(1/x^2, x, 1, inf); |
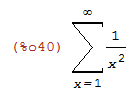
Para que o máxima simplifique o somatório, temos que adicionar a opção simpsum=true:
| (%i41) | sum(1/x^2, x, 1, inf),simpsum=true; |

O máxima é manipula somatórios, mas em geral não os contraí:
| (%i42) |
soma1: sum(1/x^2, x, 4, inf)$ soma2: sum(1/x^3, x, 2, inf) $ soma1+soma2; |
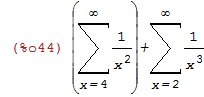
Para que o maxima agrupe os somatórios usamos o comando sumcontract:
| (%i45) | sumcontract(%); |
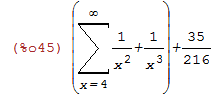
E para calcular o valor do somatório anterior:
| (%i46) | float(%,simpsum=true); |
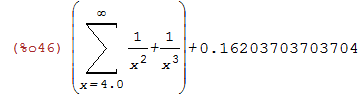
O próxima exemplo nos retorna as fórmulas fechadas para a soma dos n primeiros números,
dos quadrados dos n primeiros números, dos cubos, e da quarta potência. O comando simpsum=true
| (%i47) | [sum(i,i,1,n), sum(i^2,i,1,n), sum(i^3,i,1,n),sum(i^4,i,1,n)], simpsum=true; |
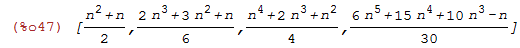
2.8 Listas
Definindo uma lista com os elementos $1,3,5,7,9$ nessa ordem:
| (%i48) | [1,3,5,7,9]; |
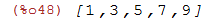
Elevando todos os elementos da lista anterior ao quadrado:
| (%i49) | [1,3,5,7,9]^2; |
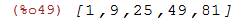
Somando os elementos de duas listas de mesmo tamanho:
| (%i50) | [2,4,6,8]+[3,5,14,22]; |
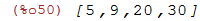
Atribuindo uma lista a uma variável:
| (%i51) | lista:[2,4,6,8]$ |
(Note que ocultamos a saída anterior, utilizando o carácter $
Somando 3 a cada elemento da lista:
| (%i52) | lista+3; |
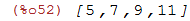
Calculando (a^+1)/(a^2) para cada elemento da lista
| (%i53) | (lista+1)/lista^2; |
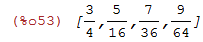
Calcular sen(x) para os elementos da lista
| (%i54) | sin(lista); |
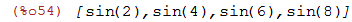
Convertendo os valores da saída anterior para ponto flutuante:
| (%i55) | %,numer; |
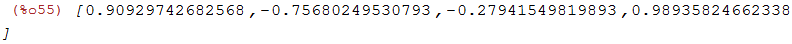
Para criar uma lista onde os elementos são definidos por uma expressão, podemos usar o comando
makelist.
Para criar a lista onde os elementos são da forma 1/n com $n$ de 1 até 8:
| (%i56) | makelist(1/n,n,1,8); |
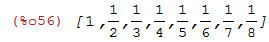
Para criar uma lista com os 10 primeiros impares:
| (%i57) | makelist(2*n+1,n,0,10); |
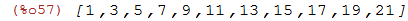
Para criar a lista onde os elementos são da forma n/(n+1) com n de 1 até 5:
| (%i58) | makelist(n/(n+1),n,1,5); |
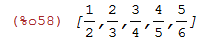
2.9 Manipulando Elementos de uma Lista
Vamos começar limpando todas as variáveis e definições, usando o comando kill(all)
| (%i59) | kill(all); |
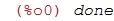
Vamos criar uma lista:
| (%i1) | lista:makelist(n^2,n,1,7); |
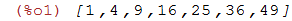
Os elementos de uma lista são indexados a partir de um. Para retornar o enésimo elemento de uma lista usamos
o comando lista[n].
| (%i2) | lista[1]; |
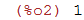
| (%i3) | lista[4]; |
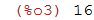
| (%i4) | lista[7]; |
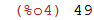
O comando rest(n) cria uma nova lista com os n primeiros elementos de uma lista removidos:
| (%i5) | listamenor: rest (lista, 3); |
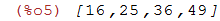
Note que a lista inicial permanece inalterada:
| (%i6) | lista; |
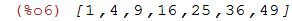
O comando append(lista1, lista2) cria uma nova lista incluindo todos os elementos de
lista1 e lista2 seguidos, incluindo os elementos da lista mais longa.
| (%i7) | lista1:[a,b,c,d]; lista2:[1,2,3,4,5,6]; |
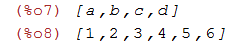
| (%i9) | append(lista1,lista2); |
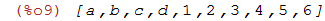
os comandos cons e endcons permitem adicionar novos elementos a uma lista, no
início e final de mesma, respectivamente;
| (%i10) | cons(X,lista1); |
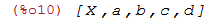
| (%i11) | endcons(X,lista1); |
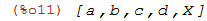
O comando delete apaga todas as ocorrências da entrada a em uma lista
| (%i12) | delete(a, [a,b,c,a,a,b]); |
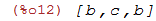
É possível realizar operações elementares, tais como a soma, subtração, multiplicação,
com os elementos de uma lista:
Vamos calcular a soma dos 20 primeiros pares
| (%i13) | pares:makelist(2*n,n,1,20); |
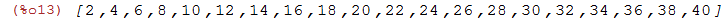
Para somar os elementos da lista usamos o comando apply
| (%i14) | apply("+", pares); |
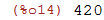
Para calcular o produto dos vinte primeiros pares:
| (%i15) | apply("*", pares); |
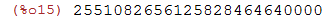
Para aplicar uma função a cada elemento de uma lista utilizamos o comando map:
Para calcular a raiz quadrada dos elementos da lista [1,6,9,13]:
| (%i16) | map(sqrt,[1,6,9,13]); |
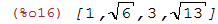
Assim por exemplo se f(x)=x+sin(x) e queremos calcular os valores de f(x) para os elementos da lista [1,2,5,7]:
Começamos definindo a função f(x) (falaremos mais sobre como definir funções)
| (%i17) | f(x):=x+sin(x); |
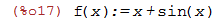
Agora aplicamos f(x) a lista
| (%i18) | map(f,[1,2,5,7]); |
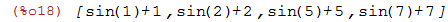
2.10 Matrizes
No Maxima define uma matriz do seguinte modo A: matrix (lista1,lista2,..,listan);
| (%i19) | A:matrix([1,2,3],[3,-1,0],[4,2,1]); |

Vamos definir outra matriz:
| (%i20) | B: matrix ([1, -1, 2], [2, 1, 5], [0, 1, 3]); |

Podemos calcular a soma $A+B$ e o produto $AB$
| (%i21) | A+B; A.B; |

Cuidado o comando A*B calcula o produto coordenada a coordenada e não o produto de matrizes:
| (%i23) | A*B; |

| (%i24) | C:matrix([2,1],[2,0]); |
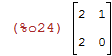
| (%i25) | C.C; |
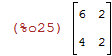
| (%i26) | C*C; |
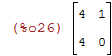
A Matriz identidade n por n pode ser facilmente definida usando o comando ident(n)
| (%i27) | ident(3); |

Se uma matriz for invertível, sua inversa pode ser calculada através do comando invert
| (%i28) | Z:invert(A); |

| (%i29) | Z.A; |

A transposta de uma matriz pode ser calculada através do comando transpose:
| (%i30) | transpose(C); |
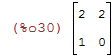
O determinante de uma matriz pode ser calculado atraves do comando det
| (%i31) | determinant(A); |
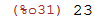
A entrada (2,3) da matriz A pode ser obtido através do comando:
| (%i32) | A[2,3]; |
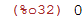
A terceira linha da matriz pode ser obtida através do comando:
| (%i33) | row(A, 3); |
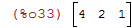
A primeira coluna de uma matriz pode ser obtida através do comando:
| (%i34) | col(A,3); |
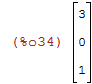
Uma matriz pode ser escalonada através do comando triangularize
| (%i35) | M:matrix([1,2,3,4],[5,6,7,z],[b,1,2,3]); |

| (%i36) | triangularize(M); |
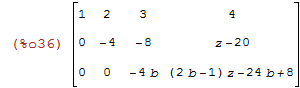
Uma matriz pode ser escalonada com $1$ nos pivôs através do comando echelon
| (%i37) | echelon(M); |
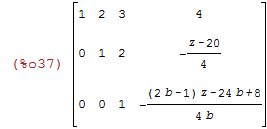
2.11 Usando o Help
O manual on-line de utilizador do Maxima pode ser visto em diferentes formas. A partir da linha de comando interativa do Maxima, o manual de utilizador é visto em texto plano através do comando \comando(?) .
O comando "? palavra" encontra um item com título igual a palavra, se existir tal item.
| (%i38) | ? limit; |

O comando "?? palavra" encontra todos os itens documentados que contiverem a palavra em seus títulos.
Se existe mais de um de tal item, Maxima solicita ao utilizador selecionar um item ou mais itens para mostrar.
| (%i39) | ?? integ; |

O comando example(tópico) mostra alguns exemplos do tópico em questão:
| (%i40) | example(limit); |

Created with wxMaxima.