1 Gráficos com o Maxima
1.1 Primeiros Gráficos
Como primeiro exemplo, vamos plotar a parabola f(x)=x^2.
| (%i33) | wxplot2d(x^2,[x,-2,2]); |
Agora vamos trocar o intervalo do domínio que estamos usando para esboçar o gráfico:
no lugar de ? e ?? coloque os valores iniciais e finais do intervalo que você deseja usar para esboçar o gráfico.
| (%i34) | wxplot2d(x^2,[x,?,??]); |

Agora vamos limitar o intervalo em y:
| (%i34) | wxplot2d(x^2,[x,-2,2],[y,0,3]); |
Agora vamos comparar os gráficos de x^2 e x^3. Para isso vamos esboçar os gráficos simultaneamente:
| (%i35) | wxplot2d([x^2,x^3],[x,-2,2]); |
Agora vamos comparar os gráficos de x^(1/2) e x^2,
| (%i36) | wxplot2d([x^(1/2),x^2],[x,0,2]); |
1.2 Gráficos das Funções Trigonométricas:
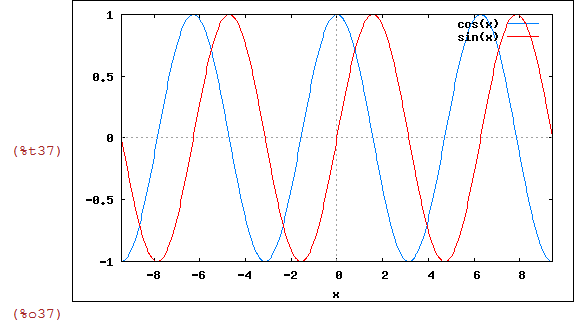
Vamos esboçar os gráficos de sen(x) e cos(x)
| (%i37) | wxplot2d([cos(x),sin(x)],[x,-3*%pi,3*%pi]); |
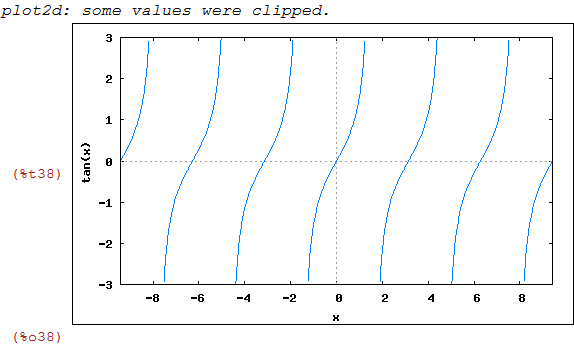
O gráfico de tangente. Nesse exemplo é fundamental delimitarmos o y, pois a função cresce indefinidamente
nos pontos da forma %pi+2*k*pi
| (%i38) | wxplot2d([tan(x)],[x,-3*%pi,3*%pi],[y,-3,3]); |
1.3 Exponencial e Logaritmo:
Gráfico de 2^x e 3^x
| (%i39) | wxplot2d([2^x,3^x],[x,-2,2]); |
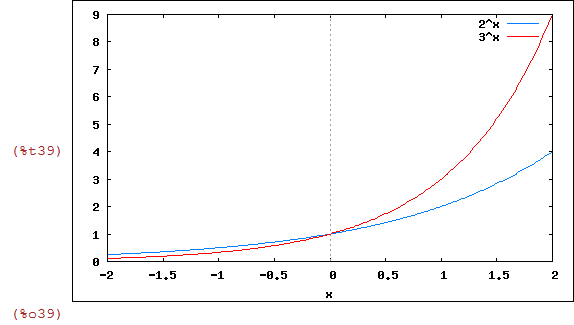
Gráfico de 2^x e (1/2)^x
| (%i40) | wxplot2d([2^x,(1/2)^x],[x,-2,2]); |
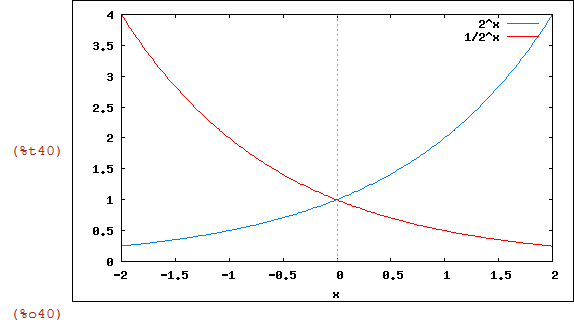
Gráfico de 2^x, e^x e 3^x
| (%i41) | wxplot2d([2^x,%e^x,3^x],[x,-2,2]); |
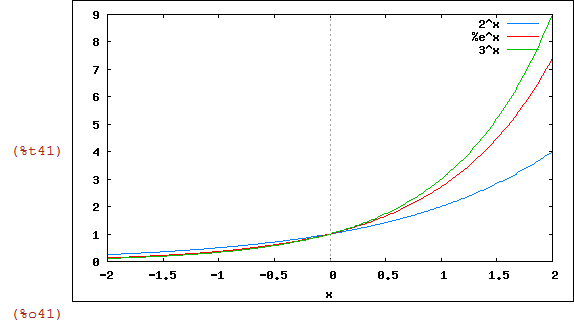
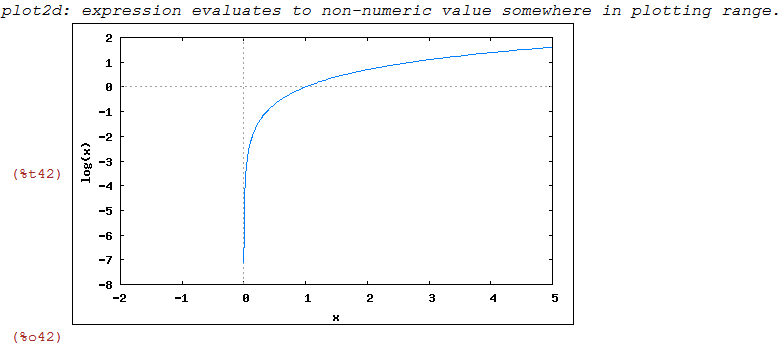
Gráfico do logaritmo na base natural, i.e, %e
| (%i42) | wxplot2d([log(x)],[x,-2,5]); |
1.4 Outros Exemplos
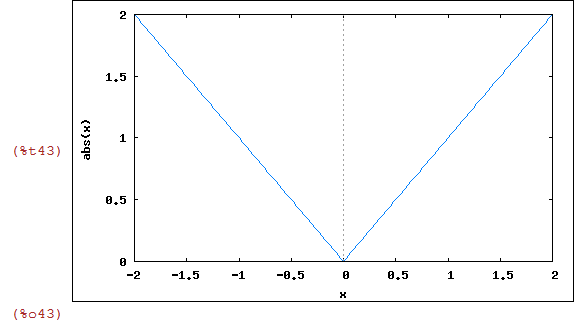
Gráfico da função módulo:
| (%i43) | wxplot2d(abs(x),[x,-2,2]); |
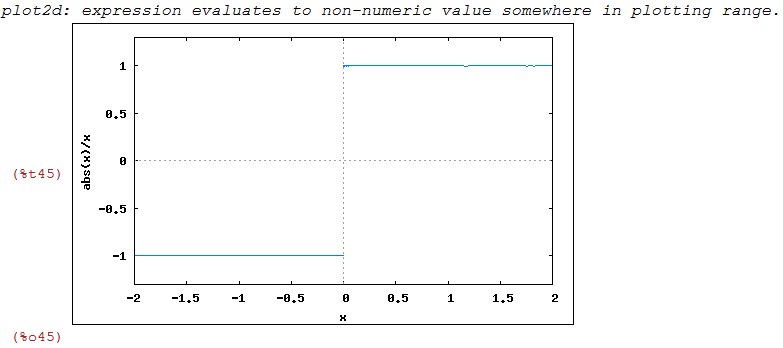
Função Sinal.
Vamos começar definindo a função sinal
sinal(x)=abs(x)/x
| (%i44) | sinal(x):=abs(x)/x; |
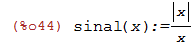
| (%i45) | wxplot2d(sinal(x),[x,-2,2],[y,-1.3,1.3]); |
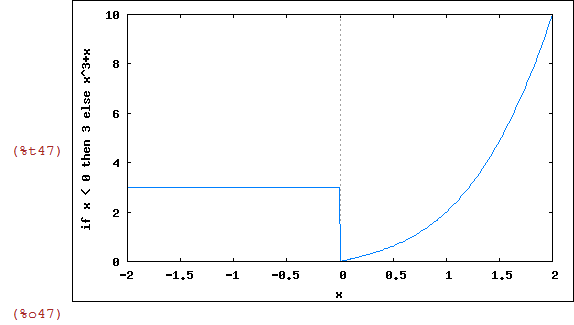
Uma função definida por partes:
|3 se x<0
g(x)= |
|x^3+x se x>=0
| (%i46) | g(x):=if x<0 then 3 else x^3+x; |
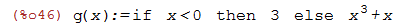
| (%i47) | wxplot2d(g(x),[x,-2,2]); |
2 Transformações de Gráficos:
2.1 Translações
Vamos visualizar o que acontece com o gráfico de h(x+c) e h(x)+c em função do gráfico de h(x).
Vamos começar definindo uma função h(x) que possui um gráfico interessante
| (%i48) | h(x):=x*cos(3*x^2)+x+1/3*x^3+sin(6*x^2); |
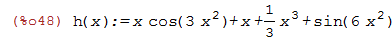
| (%i49) | wxplot2d(h(x),[x,-2,2]); |
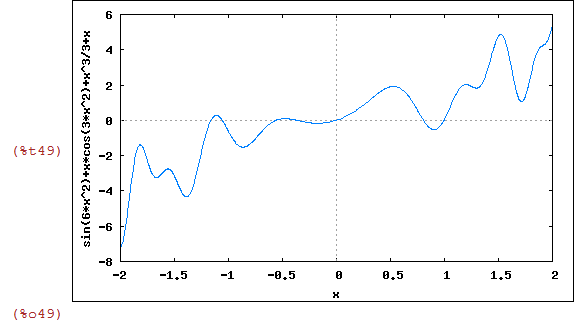
Agora vamos fazer uma lista de h(x)+c para alguns valores de c. Para ser preciso c inteiro de -1 até 1
| (%i50) | lista1:makelist(h(x)+c,c,-1,1); |
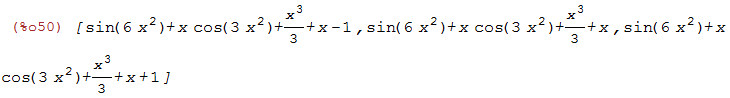
Agora vamos plotar essa lista de funções:
| (%i51) | wxplot2d(lista1,[x,-2,2],[y,-10,12]); |
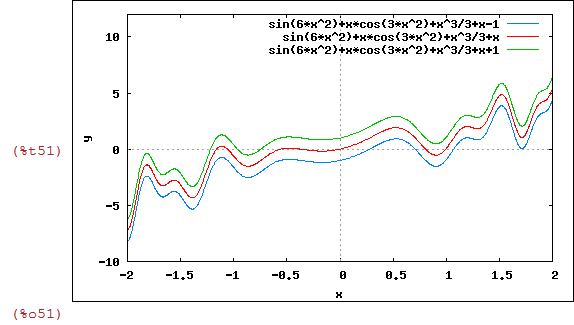
Vamos definir uma função z(x) que possui um gráfico interessante
| (%i52) | z(x):=abs(x+1/4*sin(3*x)); |
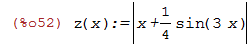
| (%i53) | wxplot2d(z(x),[x,-4,4]); |
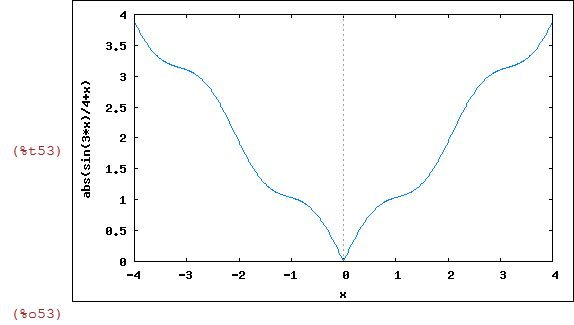
Agora vamos fazer uma lista de z(x+c) para alguns valores de c. Para ser preciso c inteiro de -1 até 1
| (%i54) | lista2:makelist(z(x+c),c,-1,1); |
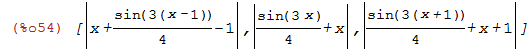
Agora vamos plotar essa lista de funções:
| (%i55) | wxplot2d(lista2,[x,-2,2]); |
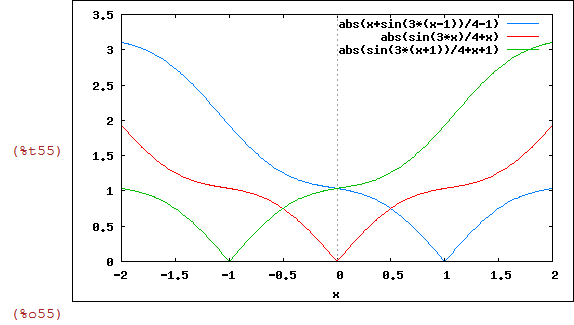
2.2 Homotetias
Vamos visualizar o que acontece com o gráfico de c*z(x). Vamos usar a função z(x) definida anteriormente.
Inicialmente uma lista de c*z(x) para alguns valores de c. Para ser preciso c será 1/2,1, 3/2 ou 2
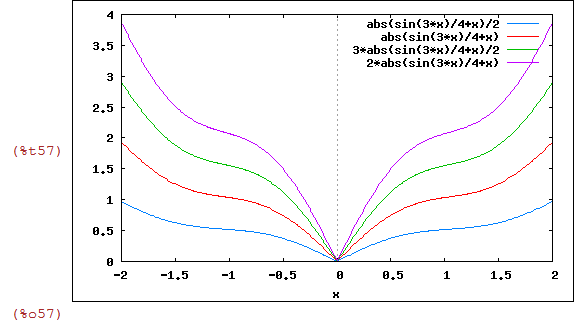
| (%i56) | lista3:makelist((d/2)*z(x),d,1,4); |
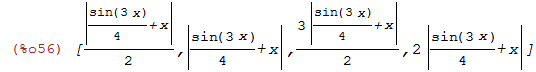
Agora vamos plotar essa lista de funções:
| (%i57) | wxplot2d(lista3,[x,-2,2]); |
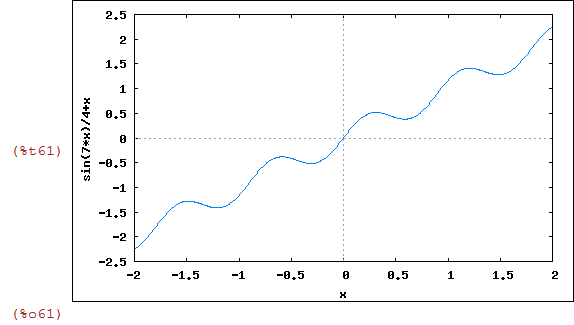
| (%i58) | w(x):=1/4*sin(x*7)+x; |
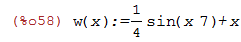
| (%i59) | wxplot2d(w(x),[x,-2,2]); |
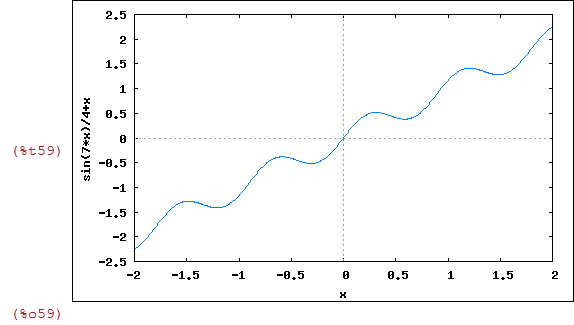
Vamos visualizar o que acontece com o gráfico de w(c*x). Vamos usar a função h(x) definida anteriormente.
Para tanto começaremos com a função w(x) definida abaixo:
| (%i60) | w(x):=1/4*sin(x*7)+x; |
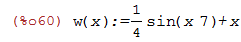
| (%i61) | wxplot2d(w(x),[x,-2,2]); |
Agora, como nos casos anteriores faremos uma lista de w(c*x) para alguns valores de c. Para ser preciso c será 1/2,1, 3/2
| (%i62) | lista4:makelist(w((d/2)*x),d,1,3); |
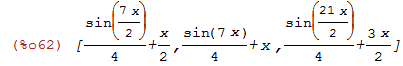
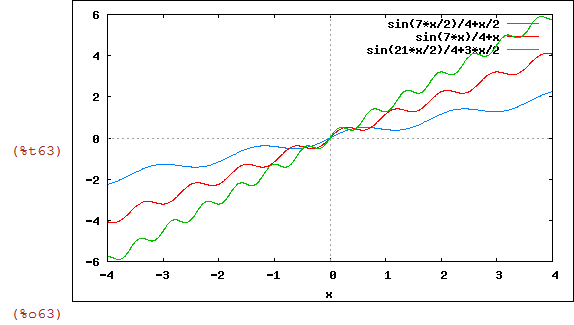
Agora vamos plotar essa lista de funções:
| (%i63) | wxplot2d(lista4,[x,-4,4]); |
2.3 Módulos
Vamos visualizar o que acontece com o gráfico de|h(x)| e h(|x|) em função do gráfico de h(x).
Gráfico de h(x)
| (%i64) | wxplot2d(h(x),[x,-2,2],); |

Gráfico de |h(x)|
| (%i64) | wxplot2d(abs(h(x)),[x,-2,2],[y,-8,8]); |
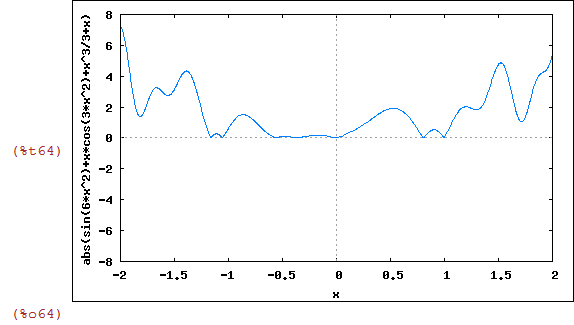
Gráfico de h(|x|)
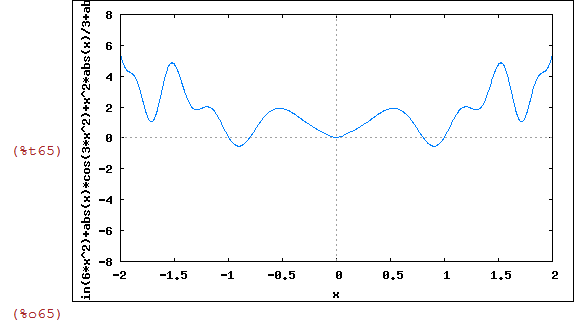
| (%i65) | wxplot2d([h(abs(x))],[x,-2,2],[y,-8,8]); |
2.4 Exercícios
Esboçe os gráficos das seguintes funções:
a) sen(2x)
b) sqrt(x^2+1)
c) 1/x+x
d) x^(1/3) on [-2,2]
e) sin(x)*x
f) |cos(x)|
g) |cos(x)|+1
h) cos(x+3) e cos(x) simultaneamente
i) cot(x) (cotangente de x) nos intervalos [x,-7,7] e [y,-5,5]
j) sec(x) (secante de x) nos intervalos [x,-7,7] e [y,-5,5]
k) x+sen(x)
l) 2^x+2^(-x) no intervalo [x,-4,4]
m) |sen(x)|
m) sen(x-1)
o)cos(2x) e cos(2x+3) simultaneamente
Created with wxMaxima.