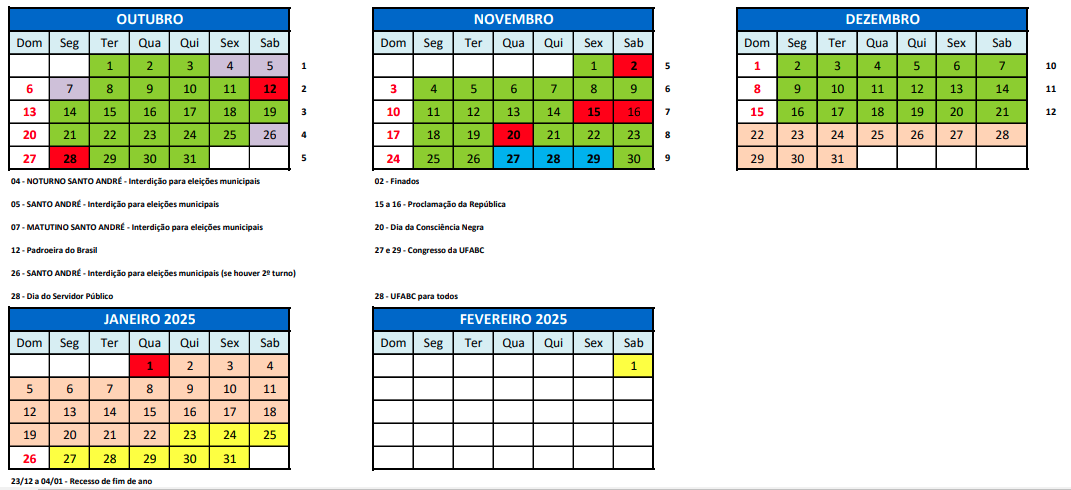
Exame 30 janeiro (repõe 15/11, sexta) das 08:00 às 10:00 na A-108
Lógica Básica 2024 - 3
Professor Jair Donadelli --- email jair.donadelli 'arroba' ufabc. ... — sala 546-2 bloco A
 Esta é uma disciplina de natureza introdutória e que não exige qualquer conhecimento prévio no estudo de lógica, porém, requer alguma experiência e maturidade matemática. Nela, o estudante tem a possibilidade de experimentar o senso de rigor conceitual e de abstração formal. O conteúdo expõe alguns aspectos da interrelação entre temas de lógica, matemática e computabilidade. Não são abordados aspectos filosóficos da Lógica.
Esta é uma disciplina de natureza introdutória e que não exige qualquer conhecimento prévio no estudo de lógica, porém, requer alguma experiência e maturidade matemática. Nela, o estudante tem a possibilidade de experimentar o senso de rigor conceitual e de abstração formal. O conteúdo expõe alguns aspectos da interrelação entre temas de lógica, matemática e computabilidade. Não são abordados aspectos filosóficos da Lógica.
Se está matriculado, atente para seu email institucional, as comunicações são feitas via siga.
Tuma DA1NHI2049-13SA Horário terças das 10:00 às 12:00; sextas das 08:00 às 10:00. Local A-108
Atendimento sexta a partir das 10:05 ou em horário combinado previamente.
ÍNDICE
Lógica Básica 2024 - 3Programação EmentaObjetivos Referências bibliográficasBásicasComplementaresAvaliação e FrequênciaLinks
Programação
| Semana | Tema | Subtemas | Atividades |
|---|---|---|---|
| 01 | Apresentação e sintaxe da linguagem da lógica proposicional | Uma visão geral de linguagem, metalinguagem, sistemas lógicos. Definição indutiva de conjuntos. Alfabeto e fórmulas. Recursos metalinguisticos para simplificação, abreviaturas e omissão de parênteses. | - leitura - exercícios |
| 02 | Sistema dedutivo axiomático do tipo de Hilbert para a lógica proposicional. | Axiomas e regra de inferência. Prova, dedução. Regras derivadas. Propriedades da Dedução | - leitura - exercícios |
| 03 | Semântica da linguagem da lógica proposicional | Valoração e interpretação. Consequência semântica. | - leitura - exercícios |
| 04 | Semântica da linguagem da lógica proposicionalMetateoremas da lógica proposicional | Equivalência semântica. Argumentos válidos. Correção do sistema proposicional. | - leitura - exercícios |
| 05 | Prova 1 na aula da sexta | Consistência e completude do sistema proposicional. conteúdo da P1 é até Argumentos válidos | |
| 06 | Metateoremas da Lógica de Proposições | Consistência e completude do sistema proposicional. Sintaxe da lógica de predicados. | o material dessa semana está dividido entre as semanas anterior e a próxima. |
| 07 | Lógica de Predicados, linguagem genérica de 1ª ordem | Sintaxe da lógica de predicados. | - leitura - exercícios |
| 08 | Lógica de Predicados | Sistema dedutivo axiomático do tipo de Hilbert. | - leitura - exercícios |
| 09 | Lógica de Predicados | Teoria formal de primeira ordem. Semântica tarskiana. | - leitura: 3ª , 6ª |
| 10 | Lógica de Predicados | Semântica: satisfazibilidade, consequência lógica. | - leitura - exercícios |
| 11 | Prova 2 na aula da sexta | ||
| 12 | Prova sub (terça) e Exame de recuperação (sexta) |
Ementa
Cálculo sentencial (ou proposicional) clássico: noções de linguagem, conectivos, dedução e teorema, semântica de valorações. Cálculo clássico de Proposições de primeira ordem: os conceitos de linguagem de primeira ordem, igualdade, teorema da dedução, conseqüência sintática. Semântica: noções de interpretação, verdade em uma estrutura, modelo. O conceito formal de teoria, fecho dedutivo. Exposição informal de temas, e.g.; acerca da consistência de teorias, completude de teorias.
Objetivos
Introdução a alguns conceitos e teoremas da lógica clássica de primeira-ordem e, também, exposição de seus significados e usos, e.g., na atividade conceitual em matemática e computação. Explicitam-se as concepções de prova lógica, de caracterização abstrato-formal de relação e objeto, de rigor, de abstração e de linguagem.
Pretende-se estabelecer certa familiaridade com a noção de sistema lógico e, então, com uma teoria de inferência dedutiva, indicar os contornos de certos pressupostos próprios do método dedutivo, também, a utilização da noção de verdade e métodos de semântica abstrato-formal.
Referências bibliográficas
Notas de aula (pdf 134pp, enviem correções e sugestões, o arquivo será atualizado durante a disciplina)
Básicas
[1] Augusto Franco de Oliveira. Lógica e aritmética: uma introdução à lógica, matemática e computacional. Gradiva, 2010. [511.3 OLIVlo3].
É difícil estabelecer algumas referências bibliográficas para essa disciplina por vários motivos, mas principalmente porque a notação raramente é comum, o que pode causar muita confusão para um primeiro curso de lógica. Ademais há pouca coisa boa em português no nível que precisamos. O item [1] acima é a alternativa para contornar esses fatos, é um ótimo livro para começar a estudar lógica, porém não está disponível eletronicamente nem há muitas cópias na biblioteca. Outras alternativas, um pouco menos aderentes à ementa mas ainda assim relevante, são
[2] Rogério Augusto Dos Santos FAJARDO, Lógica Matemática. Edusp (2017).
[3] Raymond M. SMULLYAN. Lógica de primeira ordem. São Paulo: UNESP/ Discurso Editorial, 2009
Complementares
Para quem quem se sente a vontade lendo em inglês recomendo, na ordem:
[4] Stefan BILANIUK, A Problem Course in Mathematical Logic (pdf)
[5] Wolfgang RAUTENBERG, A Concise Introduction to Mathematical Logic. Livro digital (exige IP da UFABC)
[6] Moedechai BEN-ARI, Mathematical Logic for Computer Science Livro digital (exige IP da UFABC)
Uma última sugestão de livro, que seria o primeiro da lista porém não está disponível eletronicamente e não tem muitos exemplares, é
[7] Richard E. Hodel, An introduction to mathematical logic [HODEin 511.3].
Avaliação e Frequência
2 provas
É esperado uma conduta ética por parte do aluno. Aqui e aqui se tem uma boa referência do que é esperado.
Os critérios de avaliação incluem
Apresentação clara, discursiva e objetiva.
Construção correta e em ordem dos argumentos.
Atendimento às normas de correção ortográfica e gramatical.
Observância às orientações específicas da atividade e aos prazos de entrega.
Conceito final das provas: nas avaliações serão atribuídos concentos cujo resultado ao final será de acordo com a seguinte tabela
| P1 | A | B | C | D | F | A | B | C | D | F | A | B | C | D | F | A | B | C | D | F | A | B | C | D | F | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | A | B | C | D | F | |||||||||||||||||||||||||
| Final | A | A | B | C | D | A | B | B | C | D | B | C | C | C | F | C | D | D | F | F | D | D | F | F | F |
Frequência mínima de 75%.
Substitutiva. O aluno que perder uma prova por razão justificada e de acordo com o regimento da UFABC deve apresentar justificativa e manifestar o interesse em realizar uma prova substitutiva.
Recuperação. Engloba todo o conteúdo da disciplina. Só estarão aptos os alunos com frequência mínima. O aluno deve manifestar o interesse em realizar o exame após a divulgação da media das provas.
Links
[i] Plataformas digitais, Biblioteca UFABC
[ii] Como ler e estudar matemática?,Ricardo Bianconi
[iii] Material de outras ofertas: Slides, Provas, Listas