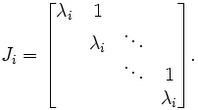
Ementa
Corpos; Espaço Vetorial sobre um corpo; Base e dimensão; Espaços Quocientes, Funcionais Lineares; Espaços Duais; Complexificação; Transformações Lineares; Espaços Invariantes; Polinômios (Anéis de Polinômios); Forma de Jordan Complexa e Real; Forma Canônica Racional.
Bibliografia
- Notas de aula
- ROMAN, S.; Advanced Linear Algebra, Springer 2005.
- KOSTRIKIN, A.I., MANIN, Y.I.; Linear algebra and geometry, Gordon and Breach 1989.
- COELHO, F.U., LOURENÇO, M.L.; Um curso de Álgebra Linear. Ed. Da Universidade de São Paulo – EDUSP. 2001.
Listas
Outros Materiais
http://hostel.ufabc.edu.br/~daniel.miranda/ala/
Média:
M=(3P1+4P2+3L)/10
- Sendo P1 a nota da primeira prova
- Sendo P2 a nota da segunda prova;
- Sendo P2 a nota da segunda prova;
- Sendo L a média das notas das listas;
Tabela de conversão média ⇨ conceito:
| Média final | Conceito |
| 0 ≤ MF < 4.5 | F |
| 4.5 ≤ MF < 5.3 | D |
| 5.3 ≤ MF < 7 | C |
| 7 ≤ MF < 8,5 | B |
| 8,5 ≤ MF < 10 | A |
A nota da prova substitutiva substituirá obrigatoriamente a menor nota tirada durante o quadrimestre.
Cronograma
Relações, Operações Binárias e Grupos. Anéis e Corpos.
- Espaços Vetoriais. Subespaços. Soma de Subespaços.
- Soma Direta. Bases Dimensão
- Decomposição em Soma Direta/ Coordenadas/ Bandeiras
- Espaços com Produto Interno.
- Transformações Lineares. Isomorfismos
- Teorema do Núcleo-Imagem
- Representação Matricial de Transformações Lineares
- Espaços Afim, Quocientes
- Teoremas de Isomorfismo.
- Espaços Duais e Aniquiladores
- Transposta/Extensão de Corpos
- Determinante
- Anéis de Polinômios
- Equivalência e Similaridade de Operadores
- Autovetores e Autovalores/ Polinômio característico e minimal.
- Teorema de Schur e Cayley-Hamilton
- Diagonalizibilidade
- Forma Canônica de Jordan.
- Forma Canônica de Jordan II
- Forma de Jordan Real/Forma Racional
- Aplicações da forma de Jordan