CVT
1º Quadrimestre de 2018
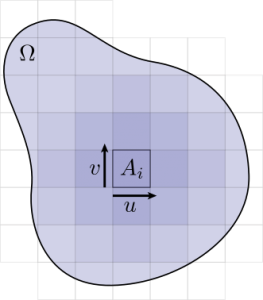
\int_{\partial \Omega}\omega=\int_\Omega d\omega.
Recomendações: Funções de Várias Variáveis
Turmas:
- Segunda das 08:00 às 10:00, sala A-102-0, semanal ,
- quarta das 10:00 às 12:00, sala A-102-0, semanal
- segunda das 10:00 às 12:00, sala A-108-0, semanal ,
- quarta das 08:00 às 10:00, sala A-108-0, semanal
Avisos:
- EXAME: dia 13/06 das 10 às 12h SALA DE AULA S 311-2 Bloco A
- Notas da P1 e P2
- Estaremos usando o moodle: https://moodle.ufabc.edu.br/
- apresentacao
- Notas de Aula em pdf (preliminar). Correções são bem vindas
- Notas de Aula – Versão para telas pequenas.
Grupo no Facebook: https://www.facebook.com/groups/calculo.vetorial.e.tensorial/
Listas de Exercício
As listas são baseadas nas listas do Márcio Fabiano, Roldão e Rodrigo Fresneda.
Avaliação
Avaliações: 2 provas, Listas (periodicidade quase semanal) e prova substitutiva.
- P1: 11 de Abril
- P2: 16 de Maio
- Sub 17 de Maio
- Exame- 1ª semana do Q3
- P1 a nota da primeira prova
- P2 a nota da segunda prova
- L a média aritmética das notas das Listas;
Provas Anteriores –
2018
2017
Ementa:
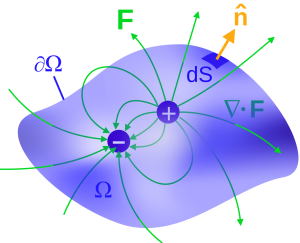
Análise Vetorial:
Campos vetoriais, operadores gradiente, divergente e rotacional. Integrais de Caminho e Superfície. Teoremas de Green, Gauss & Stokes. Teoria de Potenciais, Teorema de Helmholz.
Tensores:
Introdução ao cálculo tensorial, derivada covariante e operadores diferenciais em coordenadas curvilíneas. Aplicações do cálculo tensorial aos meios contínuos, relatividade e gravitação.
Programa
Análise Vetorial: Limites e Derivadas de Funções Vetoriais. Matriz do Jacobiano. Operadores gradiente, divergente e rotacional.
Integrais de Caminho e Superfície: Curvas e Superfícies. Integrais de Caminho e Superfície. Teoremas de Green, Gauss & Stokes. Teoria de Potenciais, Teorema de Helmholz.
Cálculo Tensorial: Introdução ao cálculo tensorial, derivada covariante e operadores diferenciais em coordenadas curvilíneas. Aplicações do cálculo tensorial aos meios contínuos, relatividade e gravitação.
Bibliografia
Parte Vetorial
- APOSTOL, T.M., Cálculo, Volume 2 (2a. edição). Editorial Reverté, 1996
- MARSDEN, J., TROMBA, A.J.; Vector Calculus, W.H. Freeman & Company, 1996.
- MATHEWS,P.; Vector Calculus, Springer 1998;
- W. Kaplan, Cálculo Avançado, Volume I. Edgard Blücher, 1991
Parte Tensorial
- Spiegel, M. R. (1959). Schaum’s outline of theory and problems of vector analysis and an introduction to tensor analysis.
- Notas de Aula em pdf (preliminar).
- MATHEWS,P.; Vector Calculus, Springer 1998;
- Análise Vetorial – Jens Mund
Referências Históricas
- CROWE, M. A History of Vector Analysis: The Evolution of the Idea of a Vectorial System
Cronograma
1 Geometria do Espaço Euclidiano
- Aula 1 Propriedades Vetoriais. Produto Interno.
- Aula 2 Produto Vetorial. Bases e Mudança de Bases;
- Aula 3 Sistemas de Coordenadas: Cilíndricas e Esféricas. Parametrizações
2 Funções Vetoriais
- Aula 4 Exemplos de funções Vetoriais. Limites e Continuidade de Funções de Rn para R m .
- Aula 5 Diferenciabilidade de Funções de R n para R m .
- Aula 6 Jacobiano
- Aula 7 Campos vetoriais e escalares. Operadores diferenciáveis: gradiente, divergente, rotacional e laplaciano.
3 Integrais de Caminho e Superfícies
- Aula 8 Integrais de Linha; Teorema Fundamental das integrais de linha.
- Aula 9 Campos conservativos. Equivalências entre campos conservativos, independência de caminho e integrais de linha sobre caminhos fechados.
- Aula 10 Área da Superfície. Integral de funções escalares em Superfícies. Integrais de Campos de Vetores
4 Os Grandes Teoremas
- Aula 11 Teorema de Green e Teorema de Stokes
- Aula 12 Teorema de Gauss
- Aula 13 Prova 1
- Aula 14 Aplicações Teoria de potenciais: potencial escalar e potencial vetor. Teorema de Helmholtz. Aplicação: Equações de Maxwell
5 Tensores
- Aula 15 Coordenadas curvilíneas. Operadores diferenciáveis em coordenadas curvilíneas.
- Aula 16 Tensores
- Aula 17 Tensores: Mudanças de Coordenadas
- Aula 18 Contrações e Tensores Simétricos e Assimétricos
- Aula 19 Aplicações: (Formas e Integrais de Formas)
- Aula 20 Aplicações (Tensor de Inércia e Outros tensores de interesse na física)
- Aula 21 Aplicações – Geometria
- Aula 22 Prova